
可視化は素晴らしいものです。ですが、優れた可視化の実現は悩ましく容易ではありません。
また、大勢に対して優れた可視化をプレゼンするような場合には時間と労力がかかりますよね。
私たちは棒グラフ、散布図、ヒストグラムの作り方についてはよく知っていますが、それらを美しくすることに対してはそこまでの注意を払っていません。
このことは同僚やマネージャーからの信頼に影響します。今あなたがそれを感じることはありませんが、それは起こることです。
さらに、私はコードの再利用が重要であることを知っています。新しいデータセットに触れるたびに一から始める必要があるでしょうか? グラフを再利用するという考え方を持つことで、私たちはそのデータに関する情報を素早く見つけることができます。
この記事で、私は三つの優れた可視化方法について話そうと思います。
- Seaborn を使ったカテゴリー相関のグラフ表現、
- ペアープロット、
- そして、スウォームプロットとグラフ注釈です。
一言でいうと、この記事では使い勝手がよくて見栄えもいいグラフを紹介します。
データを Kaggle 上の FIFA 19 完全選手データセットから拝借します。これは FIFA 19 データベースの最新版に登録されている全選手の詳細な属性をまとめたものです。
データセットには多くのカラムが含まれますが、分類があるカラムと連続性のあるカラムの一部に焦点をあてます。
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
# おそらくグリッド線は必要ないでしょう。もし必要ならこの行をコメントアウトして下さい。
sns.set(style="ticks")
player_df = pd.read_csv("../input/data.csv")
numcols = [
'Overall',
'Potential',
'Crossing','Finishing', 'ShortPassing', 'Dribbling','LongPassing', 'BallControl', 'Acceleration',
'SprintSpeed', 'Agility', 'Stamina',
'Value','Wage']
catcols = ['Name','Club','Nationality','Preferred Foot','Position','Body Type']
# カラムの一部を取り出す
player_df = player_df[numcols+ catcols]
# データの行数を少しにする
player_df.head(5)
 表:選手データ
表:選手データ
データはうまくフォーマットされていますが、私たちは Wage(賃金)と Value(価値)カラムに対して前処理をする必要があります。(ユーロ基準の値が文字列で格納されていますが)後述する分析処理のためこれを数値に直します。
def wage_split(x):
try:
return int(x.split("K")[0][1:])
except:
return 0
player_df['Wage'] = player_df['Wage'].apply(lambda x : wage_split(x))
def value_split(x):
try:
if 'M' in x:
return float(x.split("M")[0][1:])
elif 'K' in x:
return float(x.split("K")[0][1:])/1000
except:
return 0
player_df['Value'] = player_df['Value'].apply(lambda x : value_split(x))
カテゴリー相関のグラフ表現
端的に言えば、相関とは二つの変数がどのような変化を一緒にとるかという尺度です。
例えば、現実世界において、収入と支出は正の相関があります。一方が増加するときもう一方も増加します。
一方、学力とテレビゲームを遊ぶ時間には負の相関があります。一方の増加によってもう一方の減少が予測されます。
つまり、予測変数は目的変数と正もしくは負の相関がある場合に価値があります。
私は、データを理解する上で異なる変数間の相関をみることは非常に有益であると感じています。
そして Seaborn を使うことによって、非常に有益である相関のプロットを簡単に作成することができます。
corr = player_df.corr()
g = sns.heatmap(corr, vmax=.3, center=0,
square=True, linewidths=.5, cbar_kws={"shrink": .5}, annot=True, fmt='.2f', cmap='coolwarm')
sns.despine()
g.figure.set_size_inches(14,10)
plt.show()
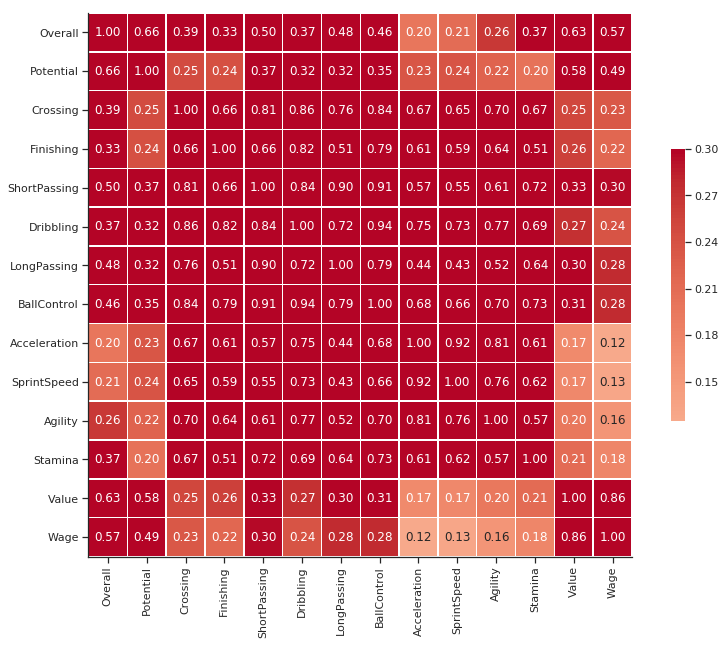
カテゴリー変数はそれぞれどのような変化をとったでしょうか?
それとは別に何か問題に気づきませんか?
はい、このグラフでは数値カラム同士の相関だけを計算しています。目的変数が Club(チーム)や Position(ポジション)だとしたらどうでしょうか?
以降の相関基準を使うことで、私たちは三つの異なった組み合わせで相関がとれるようになります。
1. 数値変数同士
ピアソン相関係数というものがあって、これは二つの変数がどのような変化を一緒にとるかという尺度になります。値のとる範囲は [-1, 1] です。
2. カテゴリー変数同士
カテゴリー変数にはクラメールの V を使いましょう。これは二つの離散変数の相互相関で、複数の段階のある変数で使われます。対称性のある尺度で変数の順序を問いません。Cramer(A,B) == Cramer(B,A) です。
例えば、今回のデータセットにおいて Club(チーム)と Nationality(国籍)にはいくらかの相関があるはずです。
これを積層グラフを使って見てみましょう。積層グラフは、カテゴリー変数同士の分布を理解するのに最適な方法です。
なお、このデータの中には国籍やチームの種類が多くありますので、私たちはその一部を扱うことにします。そこで、優秀なチーム(サンプルデータの多様性のため FC ポルトは残します)と一般性の高い国籍のみを残すことにします。
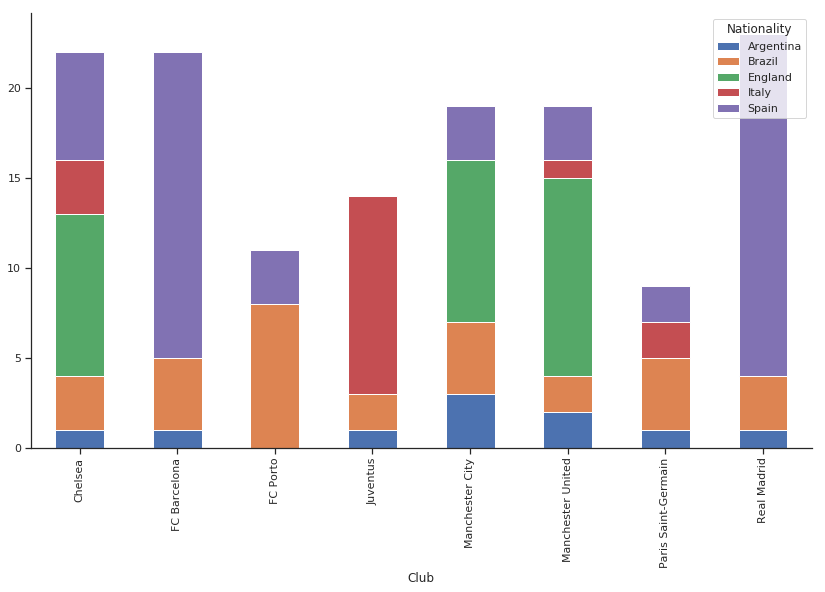
チームの選択は国籍に大きく関係していることに注目してください。前者が分かっていれば後者を予測することは非常に容易になります。
ある選手がイングランド出身であることがわかれば、その選手は FC バルセロナやバイエルンミュンヘン、ポルトではなく、チェルシーやマンチェスターユナイテッドでプレーしている可能性が高いでしょう。
つまり、ここにはある種の情報が含まれていて、クラメールの V はその情報を抽出しています。
全チームが全国籍の選手を同じ割合で保持している場合、クラメールの V は 0 です。
全チームが一つの国籍に偏って保持している場合、クラメールの V は 1 になります。例えば、イングランド出身の全選手がマンチェスター・ユナイテッドでプレイし、ドイツ出身の全選手がバイエルン・ミュンヘンでプレイするようなケースです。
それ以外のケースでは、値のとる範囲は [0, 1] です。
3. 数値変数とカテゴリー変数
分類のあるものと連続性のあるものとのケースでは、相関比率を使いましょう。
相関比率は分散に関する尺度です。多くの数式を必要としません。
ある数字が与えられる時、どのカテゴリーに分類されるかを判別することはできますか?
例を挙げて説明しましょう:
データセットから SprintSpeed(全力疾走の速さ)と Position(ポジション)の二つのカラムを使うものとします:
- ゴールキーパー:58(デ・ヘア)、52(クルトワ)、58(ノイヤー)、43(ブッフォン)
- センターバック:68(ゴディン)、59(カンパニ)、73(ウンティティ)、75(ベナティア)
- セカンドトップ:91(クリスチアーノ・ロナウド)、80(アグエロ)、76(レバンドフスキ)
ご覧の通り、これらの数字からはどのカテゴリーに分類されるかが非常に予測しやすいため、相関比率が高くなっています。
全力疾走の速さが 85 以上と分かっている時、私はその選手がセカンドトップでプレーしていると断言できます。
相関比率も [0, 1] の範囲をとります。
これをやるためのコードは dython パッケージから持ってきます。コードについてはここで多くを書きませんが、私の Kaggle カーネル上で見つけることができます。最終的な結果はこのようになります。
player_df = player_df.fillna(0)
results = associations(player_df,nominal_columns=catcols,return_results=True)
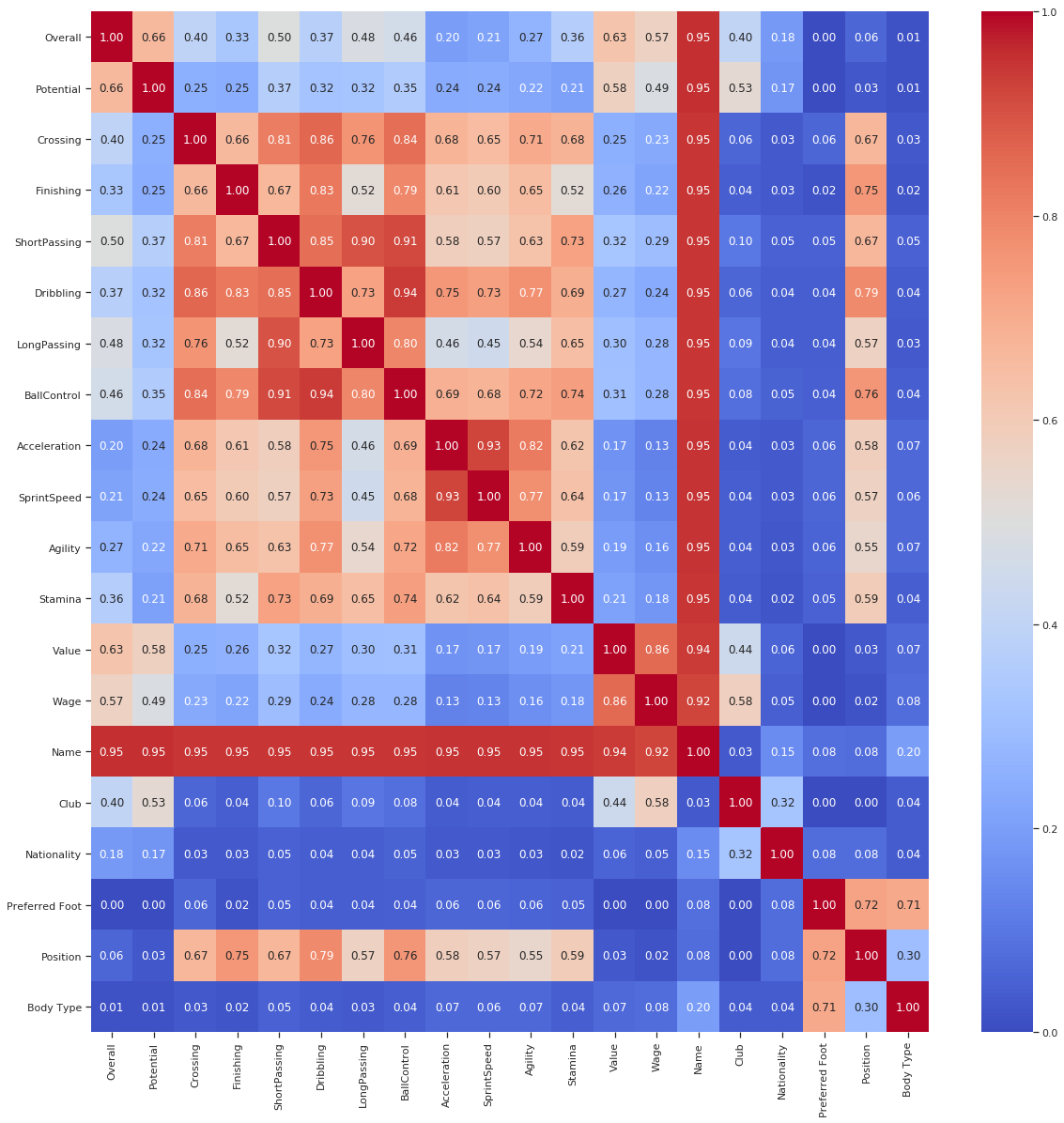 図:カテゴリー値同士、カテゴリー値と数値、数値同士の比較。非常に興味をそそられます。
図:カテゴリー値同士、カテゴリー値と数値、数値同士の比較。非常に興味をそそられます。
美しいですよね?
私たちはこのデータを見るだけで、サッカーに関してさらなる理解を得ることができます。例を挙げましょう。
選手のポジションはドリブル能力と強い相関があります。メッシが守備でプレーすることはないですよね?
選手の価値はドリブルよりもパスやボールコントロールと強い相関があります。サッカーはボールをパスし続けるスポーツです。ネイマール、私は君を見てるよ。
チームと賃金には強い相関があります。予想通りですね。
体型と利き足には強い相関があります。もしあなたが痩せ型なら、あなたは左利きである可能性が高いということでしょうか?そんなはずないですよね。調査してみてください。
それだけでなく、カテゴリー変数なしの典型的な相関のプロットではわからなかった多くの情報を、このシンプルなグラフから得ることができます。
ここでの話は以上です。表を詳しく調べてより意味のある結果を見つけるのもいいですが、これを使うことではるかに法則を見つけやすくなるというところがポイントです。
ペアープロット
私はここまで相関について多くのこと話しましたが、相関は不確定性のある測定基準です。
私の意図するところを理解してもらうために、一つの例を見てみましょう。
アンスコムのカルテットは四つのデータセットから構成されるもので、各データセットはほぼ 1 に等しい相関を持っています。しかし、それぞれ全く異なった分布をしていてグラフにすると全く違って現れます。
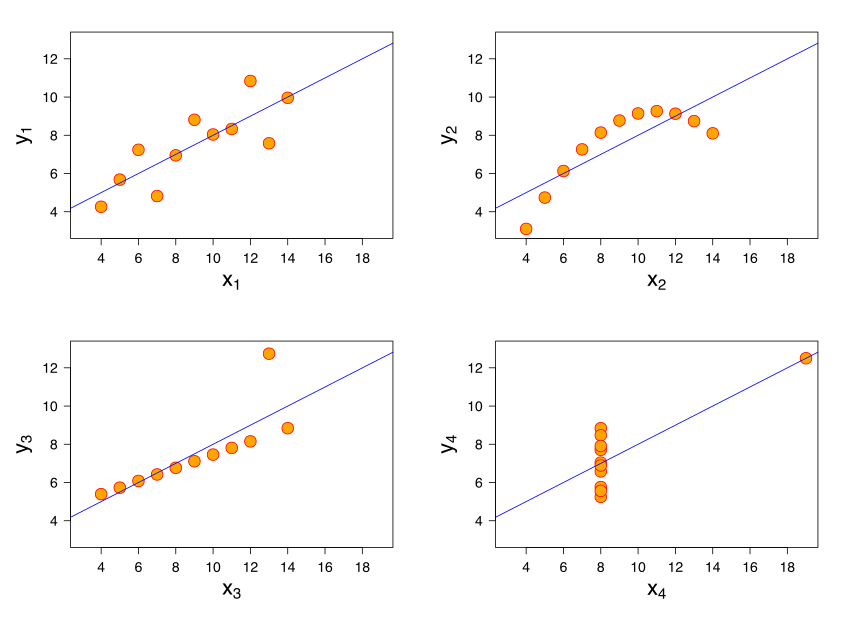 図:アンスコムのカルテット - 相関には不確定性があります。
図:アンスコムのカルテット - 相関には不確定性があります。
したがって、相関データをプロットすることが重要になることがあります。分布を個別に見てください。
現在、私たちのデータセットには多くのカラムがあります。それらを全てグラフにするのは多大な労力がかかるでしょうね。
いいえ、コードはたったの1行です。
filtered_player_df = player_df[(player_df['Club'].isin(['FC Barcelona', 'Paris Saint-Germain',
'Manchester United', 'Manchester City', 'Chelsea', 'Real Madrid','FC Porto','FC Bayern München'])) &
(player_df['Nationality'].isin(['England', 'Brazil', 'Argentina',
'Brazil', 'Italy','Spain','Germany']))
]
# ペアープロットを生成する1行
g = sns.pairplot(filtered_player_df[['Value','SprintSpeed','Potential','Wage']])
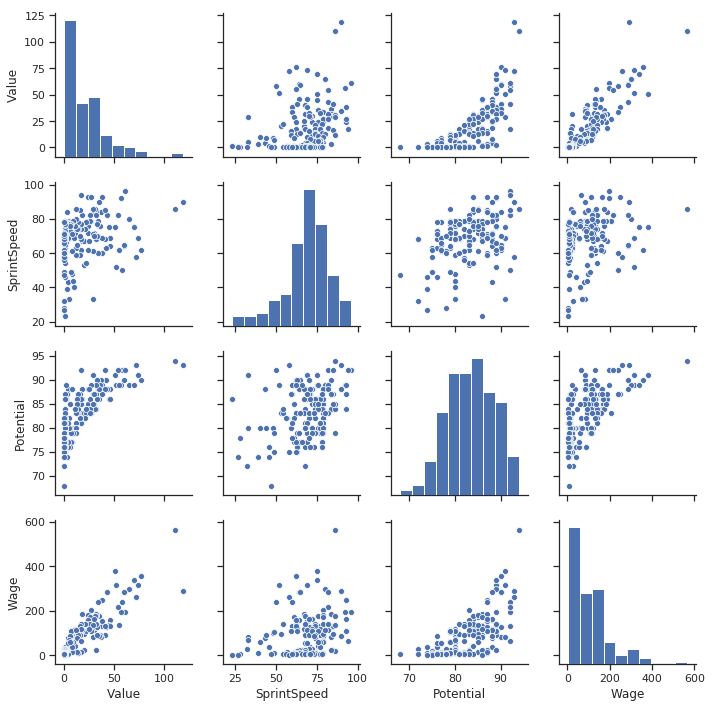
非常に良いですね。このグラフから多くのことが見てとれます。
賃金と価値は強い相関がある。
それ以外の多くの値にも相関がありますが、将来性と価値の値に関しては傾向が違います。特定のしきい値を超えた時、将来性の値がどの程度飛躍的に増加するかが見てとれます。この情報はモデリングに役立つでしょう。将来性の値に何らかの変換を加えることで、相関を強くすることはできないでしょうか?
警告: 分類のあるカラムがありません。
なにか方法はないものでしょうか?良い方法があります。
g = sns.pairplot(filtered_player_df[['Value','SprintSpeed','Potential','Wage','Club']],hue = 'Club')
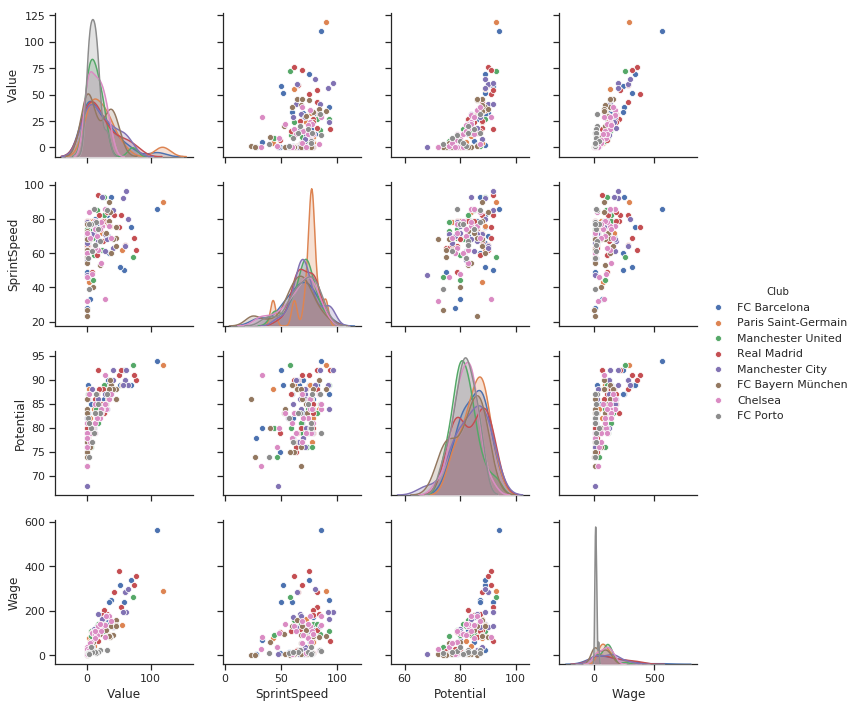
より多くの情報を得られますね。カテゴリー変数 Club(チーム)として hue パラメータを追加しただけです。
- ポルトの賃金の分布は下半分に多すぎます。
- ポルトの選手の価値に著しい分布は見られません。ポルトの選手は常に機会を伺っていることでしょう。
- 将来性と賃金のグラフ上で多くのピンク色の点(チェルシー)が固まっていることが見てとれます。チェルシーは多くの高い将来性のある選手を低い賃金で保持しています。一層の注意が必要ですね。
賃金と価値のサブプロット上にある点の中には、私が知っているものがあります。
賃金 50 万である青色の点はメッシです。また、メッシより価値の高いオレンジ色の点はネイマールです。
このハックをもってしても分類のあるカラムに関する問題は解決しませんが、カテゴリー変数の分布を見るには最高です。個別ではあるけれど。
スウォームプロット
分類のあるデータと数値データの関係性をどのように見ますか?
スウォームプロットの画像に進みましょう。その名前の通りカテゴリー単位でプロットされた点群で、Y 軸方向に若干分散させることで見やすくしています。
これはそういった関係性をプロットするものの中で、現在の私が一番気に入っているものです。
g = sns.swarmplot(y = "Club",
x = 'Wage',
data = filtered_player_df,
# 密集しないように点のサイズを小さくする
size = 7)
# グラフの上側と右側の線をなくす
sns.despine()
g.figure.set_size_inches(14,10)
plt.show()
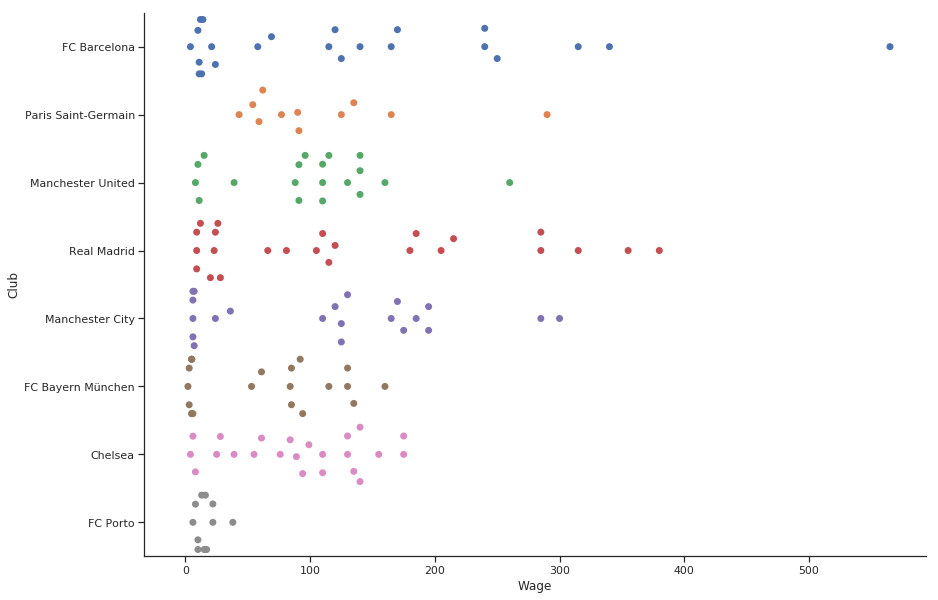
箱ひげ図も使ってみましょうか。中央値はどこ?それってプロットできるの? 答えは明白です。一番上に棒グラフを重ねれば、素晴らしい見た目のグラフが得られます。
g = sns.boxplot(y = "Club",
x = 'Wage',
data = filtered_player_df, whis=np.inf)
g = sns.swarmplot(y = "Club",
x = 'Wage',
data = filtered_player_df,
# 密集しないように点のサイズを小さくする
size = 7,color = 'black')
# グラフの上側と右側の線をなくす
sns.despine()
g.figure.set_size_inches(12,8)
plt.show()
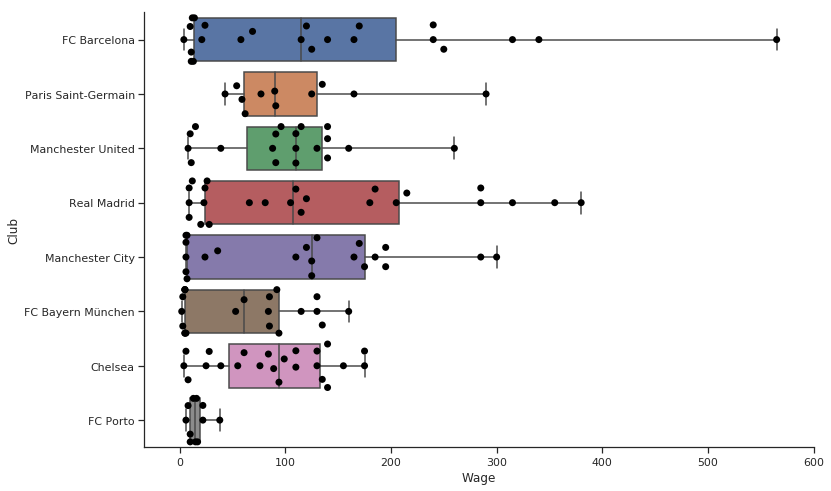
非常に良いですね。グラフ上で個々の点が見えるようになりましたし、その統計からカテゴリー単位の賃金の違いを理解することが出来ます。
右側に離れて存在する点がメッシですね。ただ、そうやって言わなくても済むように図の下にテキストで書いてあるといいですよね?
このグラフはプレゼンの場に出す予定のものです。あなたの上司は、このグラフの中にメッシと書きたいと言うでしょうね。画像注釈の出番です。
max_wage = filtered_player_df.Wage.max()
max_wage_player = filtered_player_df[(player_df['Wage'] == max_wage)]['Name'].values[0]
g = sns.boxplot(y = "Club",
x = 'Wage',
data = filtered_player_df, whis=np.inf)
g = sns.swarmplot(y = "Club",
x = 'Wage',
data = filtered_player_df,
# 密集しないように点のサイズを小さくする
size = 7,color='black')
# グラフの上側と右側の線をなくす
sns.despine()
# 注釈をつける。xy は座標で max_wage が x で 0 が y である。このプロットでは y は各レベルで 0 から 7 の範囲をとる。
# xytext はテキストを置きたいところの座標である。
plt.annotate(s = max_wage_player,
xy = (max_wage,0),
xytext = (500,1),
# 閉塞しないように矢印を縮める
arrowprops = {'facecolor':'gray', 'width': 3, 'shrink': 0.03},
backgroundcolor = 'white')
g.figure.set_size_inches(12,8)
plt.show()
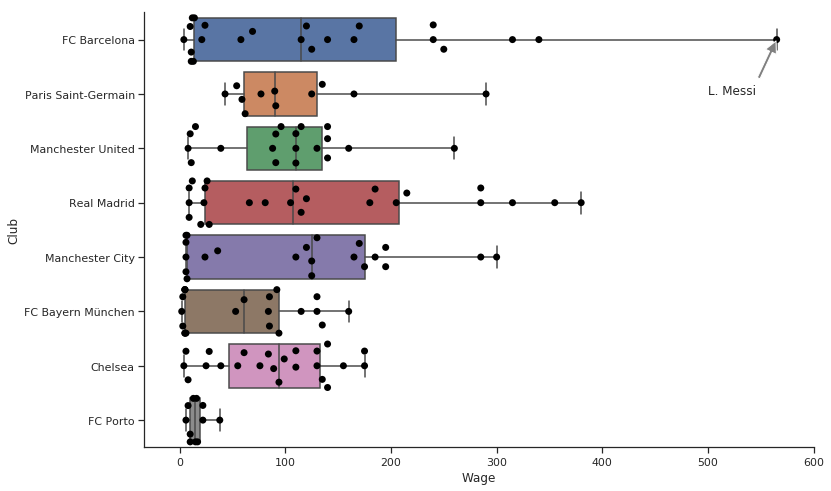
統計情報と点群の図に注釈をつけたもの。これをプレゼンに出しましょう。
- 一番下のポルトを見てください。少ない人件費で強豪と戦っています。
- レアルとバルセロナには高い額が支払われている選手が非常に多いです。
- 賃金の中間値が最も高いのはマンチェスター・シティです。
- マンチェスター・ユナイテッドとチェルシーは均等であると思います。多くの選手が同じ賃金層の近くに集まっています。
- 私はネイマールがメッシより高い価値を与えられていて嬉しいのですが、その一方でメッシとネイマールでは賃金が大きく違っています。
この世界はクレイジーですが、まともな見栄えのものが出来ました。
この記事では、異なる変数型間の相関関係を計算したり見たりすることについて要約して話すために、数値データ間の相関関係をプロットしたり、スウォームプロットを使って分類のある数値データをプロットしました。私は Seaborn でチャート要素同士をいかに重ね合わせるかを考えるのが大好きです。
可視化に関してもっと学びたければ、データ・ビジュアライゼーションコースが優れているのと、Python によるデータサイエンス専門講座という非常に優れた専門講座がありますが、そこに含まれているミシガン大学の応用プロット処理コースをお勧めします。チェックしてみてください。
もしこの記事が気に入ってもらえたなら、私の他の Seaborn に関する記事も見てみてください。より直感的で再利用可能なグラフを作っています。私は初心者向けの記事も今後書いていく予定です。通知がいくように Medium で私をフォローするか、私のブログを購読してみてください。フィードバックと建設的な批判はいつでも歓迎していて、Twitter @mlwhiz でお待ちしております。
この記事のコードは kaggle kernel からどうぞ。
